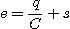
On applique la loi des mailles :
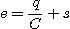
On dérive cette équation par rapport au temps :
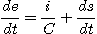
Or :
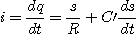
On obtient :
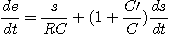
|
i) 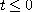
Il y a continuité de la tension aux bornes du condensateur C' d'où :
s = 0
ii) 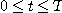
La tension d'entrée est de la forme e = kt. On a alors comme équation différentielle :
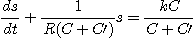
La solution de cette équation est de la forme :
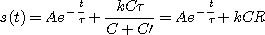
La continuité de la tension aux bornes de C' permet d'écrire :
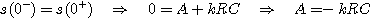
La tension s vérifie donc l'équation :
|
Comme T >> t :
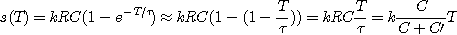
iii) t > T
Comme e = 0 l'équation différentielle s'écrit :
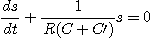
La solution de cette équation est de la forme :
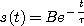
La continuité de la tension aux bornes de C' permet d'écrire :
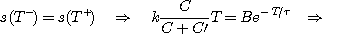
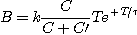
La tension s vérifie :
|